|
富山県立高校入試育英模試 第4回 「実力判定模試」
(2022年11月6日(日)実施)
|
| ◆集計人数 1,756 人(当日会場受験の1次集計人数であり、実際の申込み人数とは異なります。) |
| ◆平均点 |
| 総合 |
社会 |
国語 |
理科 |
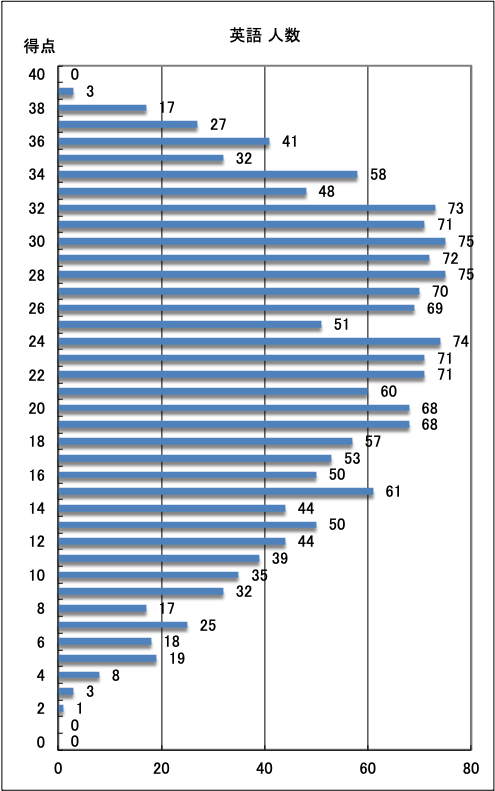
英語 |
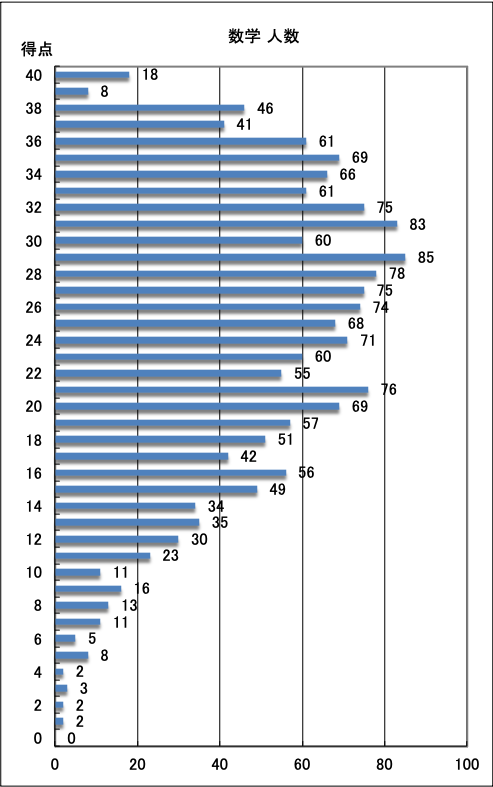
数学 |
| 128.8 |
29.6 |
26.5 |
24.9 |
22.7 |
25.1 |
|
| |
| ◆高校別志望人数表(PDFファイル)←全高校データはこちらをクリック! |
|
・高校別の今回模試の志望者数・志望者平均点・最高点を提示します。自分の志望校についての情報を手に入れよう!
|
| 富山中部・富山・高岡高校データ 抜粋 |
| 志望校 |
第一志望 |
第一志望から第三志望
までの合計 |
| 人数 |
最高点 |
平均点 |
人数 |
最高点 |
平均点 |
| 富山中部 |
普通 |
87 |
183 |
156.4 |
299 |
191 |
162.2 |
| 探究科学 |
134 |
191 |
170 |
189 |
191 |
168.5 |
| 富山 |
普通 |
173 |
176 |
148.6 |
415 |
183 |
149.7 |
| 探究科学 |
58 |
179 |
160.1 |
216 |
191 |
163.7 |
| 高岡 |
普通 |
102 |
182 |
153.5 |
194 |
191 |
154.1 |
| 探究科学 |
38 |
191 |
166.4 |
84 |
191 |
165.3 |
|
| |
| ◆得点分布表(PDFファイル)←こちらをクリック! |
|
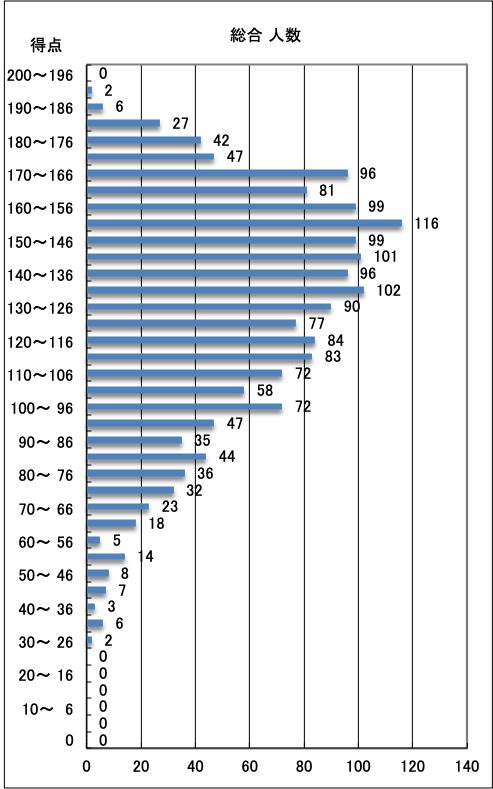
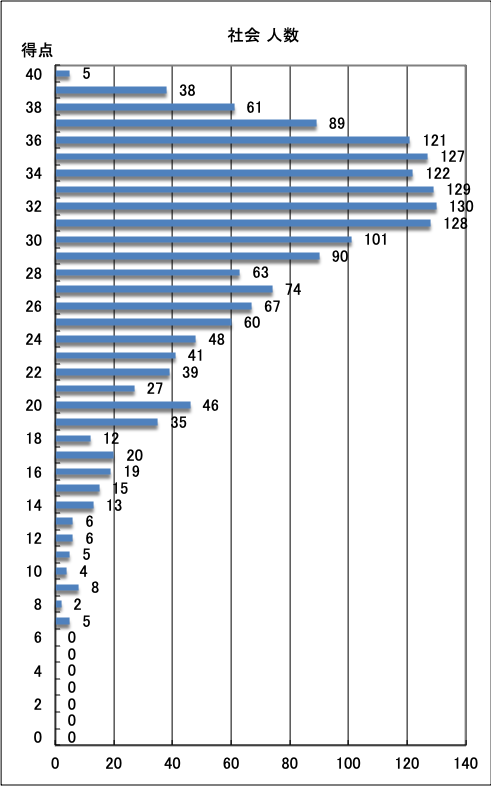
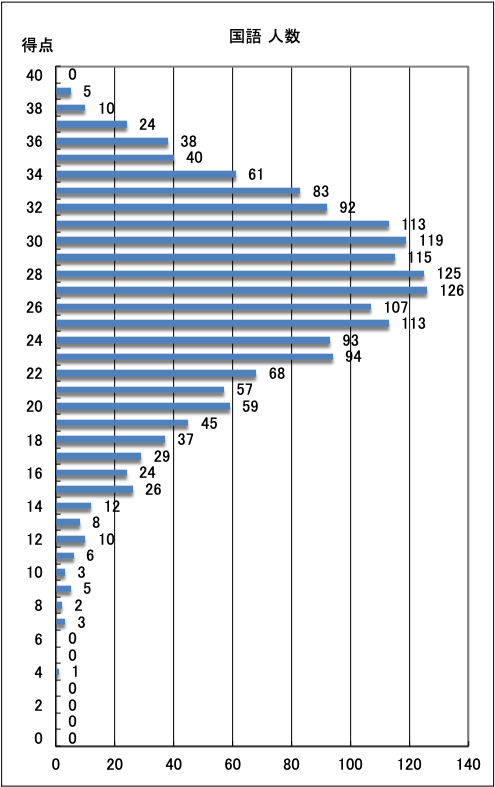
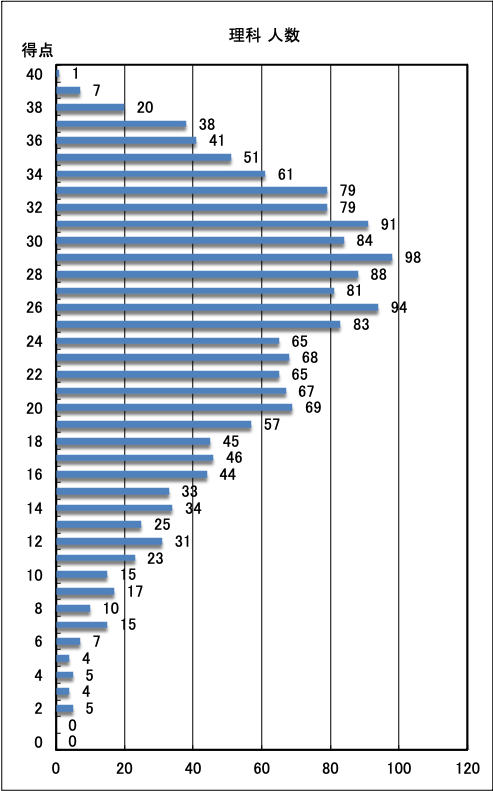
・総合,各教科の得点帯別人数表をご覧いただけます。全体順位や位置を知るのに最適です。
|
| 5教科総合 得点帯別人数グラフ |
|
|
| |
|
| ◆各教科 設問のねらい、評価項目ごとの配点・結果、得点別人数 |
| ●社会 |
| 大問別の項目 |
配点 |
設問のねらい |
| 北海道の地理 |
4
|
北海道地方の歴史と資料の読み取りができる。 |
| 東北地方地理 |
3
|
東北地方の農業や工業の特色を、資料から理解できる。 |
| アフリカ州の地理 |
6
|
アフリカ州の自然環境・人口・産業の特徴がわかる。 |
| 古墳~江戸時代の歴史 |
7
|
資料をもとに、各時代の政治や文化の様子について理解できる。 |
| 明治~平成時代の歴史 |
7
|
明治時代以降の日本と世界の歴史がわかる。 |
| 現代社会の特徴 |
6
|
現代社会に関する資料を読み取り、その特徴が理解できる。 |
| 人権と日本国憲法 |
7
|
人権と日本国憲法について理解できる。 |
|
| 評価項目 |
配点 |
平均点 |
| 北海道の地理 |
4 |
3 |
| 東北地方の地理 |
3 |
1.7 |
| アフリカ州の地理 |
6 |
5.1 |
| 古墳~江戸時代の歴史 |
7 |
5.1 |
| 明治~平成時代の歴史 |
7 |
4.6 |
| 現代社会の特徴 |
6 |
4.8 |
| 人権と日本国憲法 |
7 |
5.3 |
|
【 採点者からひとこと 】
用語を答える問題では、1(1)開拓使や4(2)①源氏物語の間違いが多く見られました。用語を正しく覚えていない、または正しい漢字で書けていないようでした。語句問題で間違えていた場合は、その用語の意味などについてもしっかりと確認し、一問一答の問題演習で定着を図りましょう。
記述では、5(1)徴兵令の説明で対象となる年齢や性別が他の内容のものを混同している答案が多く見られました。用語問題同様もう一度教科書で内容を確認しましょう。また、誤字・脱字は内容が正しくても×になります。必ず見直しの時間をつくりましょう。
今回から公民分野も出題されましたが、正答率は高かったです。引き続き学校の1回1回の授業を大切にし、入試まで学び残しが無いようにしておきましょう。 |
| 【福光校・中田】
|
|
|
|
| |
| ●国語 |
| 大問別の項目 |
配点 |
設問のねらい |
| 漢字の読み書き |
6
|
既習の漢字を正確に読み書きできる。 |
| 説明的文章(論説文) |
12
|
筆者の主張や考えを正しく読み取ることができる。 |
| 文学的文章(小説文) |
11
|
場面をきちんと把握し、登場人物の心情を読み取ることができる。 |
| 古典(古文) |
5
|
古文の内容を正しく読み取ることができる。 |
| 課題作文 |
6
|
条件に従って文章をまとめることができる。 |
|
| 評価項目 |
配点 |
平均点 |
| 漢字の読み書き |
6 |
4.6 |
| 説明的文章(論説文) |
12 |
7.4 |
| 文学的文章(小説文) |
11 |
6.6 |
| 古典(古文) |
5 |
2.9 |
| 課題作文 |
6 |
5 |
|
【 採点者からひとこと 】
漢字は「折衝」の読みの正答率が低かったようです。読みが分からない時は、その漢字を使った別の熟語を考えることも有効です。例えば、右折の「セツ」と衝突の「ショウ」の組み合わせとして考えると、正答が浮かぶこともあります。
記述問題においては、二の4のⅡで間違いが多く見られました。問いかけが、「可能になるのはどのようなことか」なのに対し、「~できること」などの可能動詞を用いて答えてはいけません。聞かれ方に対する答え方を常に意識してきましょう。
古文は比較的読みやすい文章であり、全体的に良くできていたようです。これからも様々な古文に触れ、入試本番でも確実に得点してください。 |
| 【富山本部校・田中】
|
|
|
|
| |
| ●理科 |
| 大問別の項目 |
配点 |
設問のねらい |
| 生物の成長と細胞分裂 |
5
|
植物の成長のし方と、体細胞分裂の過程が理解できる。 |
| 圧力の計算 |
5
|
圧力について理解し、作図問題や計算問題を解くことができる。 |
| 地層 |
5
|
堆積岩のでき方や特徴がわかる。地層から大地の変化を読み取ることができる。 |
| 状態変化 |
5
|
状態変化と質量・体積・密度の関係を正しく理解できる。蒸留の実験の手順や結果がわかる。 |
| 物体の運動 |
5
|
力がはたらく運動とはたらかない運動の違いを理解し、区別することができる。 |
| 塩化銅の電気分解 |
5
|
塩化銅水溶液の電気分解実験の手順や結果について理解できる。質量を求める計算ができる。 |
| 光合成 |
5
|
光合成のしくみを理解し、実験の手順や結果についてわかる。 |
| 日本の天気 |
5
|
日本周辺の四季の変化とその原因を理解し、天気図からその特徴を読み取ることができる。 |
|
| 評価項目 |
配点 |
平均点 |
| 生物の成長と細胞分裂 |
5 |
4 |
| 圧力の計算 |
5 |
2.6 |
| 地層 |
5 |
3.7 |
| 状態変化 |
5 |
3.1 |
| 物体の運動 |
5 |
3.1 |
| 塩化銅の電気分解 |
5 |
1.9 |
| 光合成 |
5 |
3.5 |
| 日本の天気 |
5 |
3 |
|
【 採点者からひとこと 】
今回の模試では,富山県の県立入試問題にあわせて,基本事項を確認する問題を中心に、いくつか思考力の必要な問題を出題しました。「状態変化」や「光合成」、「日本の天気」など、1、2年の学習内容からの基本的な出題でも正答率が低い問題がいくつか見られました。富山県の県立入試は1~3年の学習内容からほぼ偏りなく出題されます。解けない単元がある生徒は早急に見直しを行い,苦手を無くしていきましょう。
また、「圧力の計算」や「塩化銅の電気分解」などの計算問題では正答率が非常に低くなっていました。比較的難易度の高い問題ですが、解き方のパターンを覚えていれば、対応できます。県立入試まであきらめずにいろいろな問題に取り組んでみましょう。 |
| 【砺波校・大野】
|
|
|
|
| |
| ●英語 |
| 大問別の項目 |
配点
|
設問のねらい |
| 【聞き取りテスト】 |
| 聞くこと |
10
|
英語の説明や対話を聞いて、内容が理解できる。 |
| 【筆記テスト】 |
| 1.話すこと |
10
|
さまざまな形式の対話文を読んで、内容が理解できる。 |
| 2.読むこと |
9
|
いろいろな長文を読んで、内容が理解できる。 |
| 3.書くこと |
11
|
さまざまな場面や内容に応じて、英語で表現できる。 |
|
| 評価項目 |
配点 |
平均点 |
| 聞くこと/リスニング |
10 |
6 |
| 話すこと |
10 |
6.5 |
| 読むこと |
9 |
5 |
| 書くこと |
11 |
5.2 |
|
【 採点者からひとこと 】
新学習指導要領により、中学生に求められる英語のレベルが上がりました。その影響で県立入試も難易度が上がっています。その中で、点数を取るべきところで取らないと、合計点が伸びなくなってしまします。今回感じたのは、リスニングや筆記の大問1で出題された、曜日・季節のスペルミスです。これらの単語は小学校で既に学習しているものとされており、当然中学生は綴りをミスなく書けなければなりません。英単語・英文法共に基本に立ち返り、自分が解ける!と感じる問題でミスをしないよう注意していきましょう。 |
| 【城南本部校・田中】
|
|
|
|
| |
| ●数学 |
| 大問別の項目 |
配点
|
設問のねらい |
| 基本問題 |
11
|
各単元における基本的な内容が理解できる。 |
| 放物線 |
4
|
関数の性質を理解して、座標や直線の式を求めることができる。 |
| 2次方程式 |
4
|
与えられた条件により2次方程式をつくり、解くことができる。 |
| 空間図形 |
5
|
いろいろな立体の表面積や体積を求めることができる。 |
| 規則性 |
5
|
図形の並び方の規則性を理解して、応用することができる。 |
| 平面図形 |
5
|
与えられた条件をもとに、三角形の合同を証明することができる。
証明した三角形の性質を利用して、三角形の面積を求めることができる。 |
| 関数の応用 |
6
|
時間と移動距離を関数としてとらえ、式に表したり、応用したりすることができる。 |
|
| 評価項目 |
配点 |
平均点 |
| 基本問題 |
11 |
8.9 |
| 放物線 |
4 |
2.9 |
| 2次方程式 |
4 |
2.4 |
| 空間図形 |
5 |
2.3 |
| 規則性 |
5 |
2.8 |
| 平面図形 |
5 |
2.9 |
| 関数の応用 |
6 |
2.9 |
|
【 採点者からひとこと 】
今回の模試は,入試傾向を踏まえ,方程式,関数,図形など各分野から満遍なく出題しました。
関数 у=ax2 は,放物線と直線を出題しましたが,比例定数や座標など基本的なことは,求められるようにしましょう。規則性の問題では,式で表すことより,実際に出てくる数の規則を理解して考える内容の問題を出題しました。表や図を参考にして,規則をしっかり把握しましょう。1次関数の応用では,ダイヤグラムの問題を出題しましたが,今回は最終問題で,グラフの規則性(反復性)から,走行距離を考える問題も出題しました。いろいろな応用問題の解法パターンを理解しましょう。
今後は,過去の入試問題を解いてみるなど,入試レベルの問題にも慣れていくことが大切です。計画的に学習を進めていきましょう。 |
| 【小杉校・熊野】
|
|
|
|
| |